September 8, 2015

Math and Crime: Data Models of Social Networks Can Help Police Fight Gangs

LAPD commander in front of screens — CGU mathematics Professor Allon Percus and other collaborators used methods created for solving partial differential equations to create new data classification techniques to analyze a social network of known or suspected gang members in Los Angeles. Mathematical models of such networks help explain how these groups recruit members and can assist police in identifying crime hot spots. (In this photo, Los Angeles Police Department Commander Sean Malinowski works in his agency's Emergency Operations Center. Photo by Anne Cusack/Los Angeles Times via Getty Images)

Math and Crime: In the syndicated CBS drama Numb3rs, researchers develop mathematical models that help the FBI solve crimes. In the 1993 blockbuster film Jurassic Park, a mathematician utilized his knowledge of chaos theory to correctly predict the catastrophic dangers of creating a dinosaur-themed amusement park.

In the entertainment industry, using math to fight crime and protect lives is common.

But as ongoing research taking place at CGU’s Institute of Mathematical Sciences (IMS) demonstrates, such depictions are far from imaginary. IMS Associate Professor Allon Percus, along with other researchers, is studying applied mathematics methods that could help law enforcement and national security efforts.

“Today, the tools of applied mathematics have become indispensable to help police departments predict crime and fight gang violence,” Allon Percus said.

“Ten years ago, mentioning ‘crime’ and ‘mathematician’ in the same sentence would probably have conjured up images of the Unabomber,” Percus said. “Today, the tools of applied mathematics have become indispensable to help police departments predict crime and fight gang violence.”

Percus’ collaborators include Cristina Garcia-Cardona, a CGU alumna (PhD, Mathematics, 2013); Anna Ma, an IMS doctoral student; UCLA mathematics Professor (and 2014 CGU honorary doctorate awardee) Andrea Bertozzi; and members of Bertozzi’s applied mathematics group including Blake Hunter, now an assistant professor of mathematics at Claremont McKenna College.

In 2010, Percus, along with scientists from seven other institutions, was awarded a five-year grant by the Air Force Office of Scientific Research, an agency entrusted with promoting scientific research in areas that benefit the United States’ peacekeeping and defense capabilities.

Percus’ research builds upon prior work by Bertozzi, Hunter, and others who studied Los Angeles Police Department (LAPD) data. The data—from 748 known or suspected gang members—included the times and locations they were stopped by officers, their addresses, visible gang insignias, and any individuals accompanying them. All of this information combines to form a large social network ripe for mathematical analysis, according to Percus.

Insight into how social networks form, grow, and evolve is relevant to law enforcement and military interests. Preventing acts of terrorism and crime relies on an increasingly sophisticated understanding of how such groups form and interact. Mathematical models of these networks, which describe who communicates with whom, help explain how these groups recruit and train members.

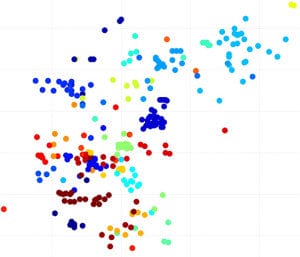
Illustration of algorithm — This image illustrates Allon Percus’ group’s algorithm that was able to analyze LAPD data and correctly identify gang members by up to 75 percent. The different colored dots represent different gangs. (*Photo courtesy of Cristina Garcia-Cardona*)

Using a data-mining technique called “spectral clustering,” Bertozzi’s group was able to identify certain social and geographical patterns that could determine, for instance, hotspots for gang violence.

Inspired by the UCLA group’s results, Percus and his colleagues used methods created for solving partial differential equations to create new data classification techniques for networks of this kind. Garcia-Cardona developed an algorithm designed to determine the gang membership of gang-affiliated individuals.

Subsequent work by Percus and Garcia-Cardona in collaboration with Hunter was able to improve the rate of correct gang membership identification from 56 percent to 75 percent.

Because there are noted parallels between gang formation and the rise of insurgencies, the techniques employed by Percus and the other researchers can suggest strategies for interrupting such networks and preventing hostile acts.

“Without the underlying mathematics,” Percus said, “today’s world would be a very different place.”